深度学习入门八----卷积神经网络

发表评论
426 views

深度学习入门八----卷积神经网络

人工神经网络是一门机器学习学科，已成功应用于模式分类、聚类、回归、关联、时间序列预测、优化等问题。随着过去十年社交媒体的日益普及，图像和视频处理任务变得非常重要。以前的神经网络架构（例如前馈神经网络）无法扩展用以处理图像和视频任务。这加速了专门为图像和视频处理任务量身定制的卷积神经网络的出现。在本篇文章中，我们将解释什么是卷积神经网络，讨论它们的架构，并用代码实现一两个简单模型。

Limitations of feedforward neural networks (FNN) for image processing

在全连接 FNN（如下图所示结构）中，一层中的所有节点都连接到下一层中的所有节点。每个连接都有一个权重 

 需要由学习算法学习。假设我们的输入是一个 64 x 64 像素的灰度图像。每个灰度像素由 1 个值表示，通常在 0 到 255 之间，其中 0 代表黑色，255 代表白色，中间的值代表各种灰度。由于每个灰度像素可以用 1 个值表示，我们说通道大小为 1。这样的图像可以用 64 X 64 X 1 = 4,096 个值（行 X 列 X 通道）表示。因此，处理此类图像的 FNN 的输入层有 4096 个节点。 我们假设下一层有 500 个节点。由于后续层中的所有节点都是完全连接的，因此输入和第一个隐藏层之间将有 4,096 X 500 = 2,048,000 个权重。对于复杂的问题，我们的 FNN 通常需要多个隐藏层，因为简单的 FNN 可能无法学习出将训练数据中的输入映射到输出的模型。具有多个隐藏层会加剧 FNN 中具有很多权重的问题。随着搜索空间维度的增加，拥有许多权重会使学习过程变得更加困难。它还使训练更加耗费时间和资源，并增加过拟合的可能性。对于彩色图像，这个问题进一步复杂化。与灰度图像不同，彩色图像中的每个像素由 3 个值表示，分别代表红色、绿色和蓝色（称为 RGB 颜色模式），其中每种颜色都可以由这些原色的各种组合表示。由于每个颜色像素可以用 3 个值表示，因此我们说通道大小为 3。这样的图像可以用 64 X 64 X 3 = 12,288 个值（行 X 列 X 通道）表示。输入层和具有 500 个节点的第一个隐藏层之间的权重数现在是 12,288 X 500 = 6,144,000。很明显，FNN 无法扩展以处理更大的图像，我们需要一个更具扩展性的架构。 图1 上图是一个带有隐藏层的前馈神经网络。为清楚起见，省略了对隐藏/输出层神经元的偏差(bias)。 使用 FNN 进行图像处理的另一个问题是，二维图像在输入层中表示为一维向量，因此忽略了数据中的任何空间关系。另一方面，CNN 维护了数据的空间结构，更适合在图像数据中寻找空间关系。

Inspiration for convolutional neural networks

1959 年，Hubel 和 Wiesel 进行了一项实验，用以了解大脑的视觉皮层如何处理视觉信息。他们在猫面前移动一条亮线时，记录了猫视觉皮层中神经元的活动。他们注意到当亮线以特定角度和特定位置显示时，一些细胞会激发（他们称之为simple cells）。另一些细胞，无论亮线处于哪个角度/位置，他们都会被激发，并且似乎可以检测到运动（他们称之为complex cells)。看起来complex cells能从多个simple cells接收输入并具有层次结构。 Hubel 和 Wiesel 因他们的发现于 1981 年获得了诺贝尔奖。 1980 年，受复杂和简单细胞层次结构的启发，Fukushima提出了 Neocognitron，一种用于手写日语字符识别的层次神经网络。 Neocognitron 是第一个 CNN，并且有自己的训练算法。 1989 年，LeCun 等提出了一种可以通过反向传播算法训练的 CNN。当 CNN 在 ILSVRC（ImageNet 大规模视觉识别挑战赛）上的表现优于其他模型时，它们获得了极大的欢迎。 ILSVRC 是一项在数百个对象类别和数百万张图像上进行对象分类和检测的竞赛。该挑战赛从 2010 年至今每年举办一次，吸引了 50 多个机构的参与。赢得 ILSVRC 的著名 CNN 架构是 2012 年的 AlexNet，2013 年的 ZFNet，2014 年的 GoogLeNet 和 VGG，2015 年ResNet。

Architecture of CNN

典型的CNN有以下4层:

  • Input layer
  • Convolution layer
  • Pooling layer
  • Fully connected layer ### Input layer 输入层代表CNN的输入。比如输入可以是 28 像素 x 28 像素的灰度图像。与 FNN 不同，我们不会将输入“展平”为一维向量，输入就是一个 28 x 28 矩阵的形式，它会以二维形式呈现给网络。这使得捕获空间关系更容易。 ### Convolution layer 卷积层由多个过滤器-filters（也称为kernels）组成。 2D 图像的过滤器也是 2D 的。假设我们有一个 28 x 28 像素的灰度图像。每个像素由 0 到 255 之间的数字表示，其中 0 代表黑色，255 代表白色，中间的值代表不同深浅的灰色。假设我们有一个 3 x 3 filter（总共 9 个值），并且这些值随机设置为 0 或 1。卷积是将 3 x 3 过滤器放置在图像的左上角，将过滤器值乘以像素值并添加到结果中，一次将过滤器向右移动一个像素并重复此过程。当我们到达图像的右上角时，我们只需将过滤器向下移动一个像素并从左侧重新开始。当我们到达图像的右下角时，这个过程就结束了。如下图所示： 图2 Covolution operator 有以下参数：
  • Filter size
  • Padding
  • Stride
  • Dilation
  • Activation function 过滤器尺寸可以是 5 x 5、3 x 3 等等。应避免使用较大的过滤器尺寸，因为学习算法需要学习过滤器值（权重），而较大的过滤器会增加要学习的权重数量（更多的计算能力、更多的训练时间、更多的过度拟合机会）。此外，奇数大小的过滤器比偶数大小的过滤器更受欢迎，因为所有输入像素都在输出像素周围具有良好的几何特性。 观察前边的图2，会看到在将 3 x 3 过滤器应用于 4 x 4 图像后，我们最终得到了一个 2 x 2 图像——图像的尺寸变小了。如果我们想保持生成的图像大小与原图像相同，我们可以使用padding(填充)。在应用filter之前，我们将0填充在输入图像的各个方向上。如果填充是 1 x 1，那么我们在每个方向上添加 1 个零。如果它是 2 x 2，那么我们在每个方向上添加 2 个零，依此类推。如下图所示，我们在5 x 5 的图像周围，添加一圈0，这样卷积之后得到的图像尺寸还是5 x 5。 图3 如前所述，我们通过将过滤器放在图像的左上角来开始卷积，在将过滤器和图像值相乘（并添加它们）之后，我们将过滤器向右移动并重复该过程。我们向右（或向下）移动多少像素就是stride(步幅)。在前边的两个例子中，过滤器的stride都是为 1。我们将过滤器向右（或向下）移动一个像素。但是我们可以使用不同的步幅。下图显示了使用 stride 为 2 的示例。 图4 当我们对图像应用 3 x 3 过滤器时，过滤器的输出会受到图像 3 x 3 子集中像素的影响。如果我们想要更大的感受野（影响过滤器输出的图像部分），我们可以使用dilation(扩张)。如果我们将dilation设置为 2，而不是图像的连续 3 x 3 子集，图像的 5 x 5 子集的每隔一个像素都会影响过滤器的输出。下边是一个将 3 x 3 过滤器应用于 7 x 7 图像，膨胀为 2，从而生成 3 x 3 的图像。 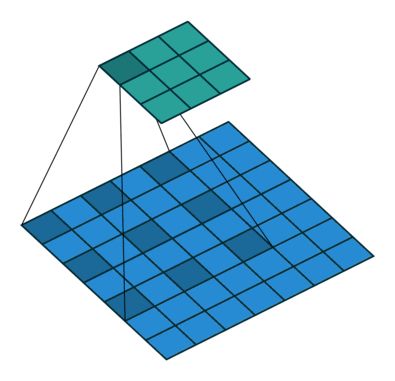图5 在过滤器扫描整个图像后，我们应用一个激活函数来过滤输出以引入非线性。 CNN 中使用的首选激活函数是 ReLU 或其变体之一，如 Leaky ReLU。 ReLU 在过滤器输出中保留具有正值的像素，并将负值替换为 0（或在 Leaky ReLU 的情况下使用少量）。下图显示了将 ReLU 激活函数应用于过滤器输出的结果。 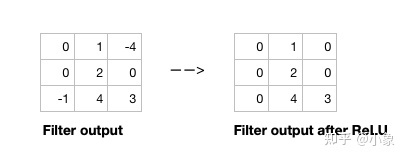图6 给定输入大小、过滤器大小、填充、步长和膨胀，您可以计算卷积运算的输出大小，如下所示。 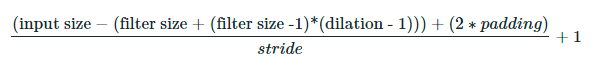图7 输入是一个单个通道 5 x 5 的向量 (5 x 5 x 1)，滤波器大小为3 x 3 ，单输入通道二维卷积示意图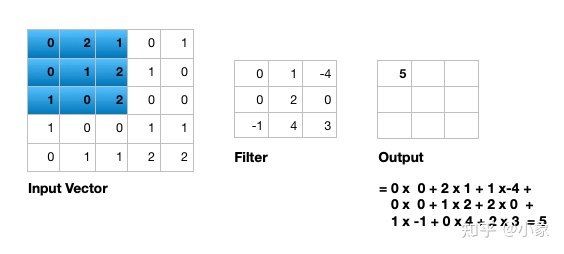： 图8 接着我们看一下输入向量具有 3 个通道 (5 x 5 x 3) 时的计算。为了在 2 维中显示这一点，我们分别在输入向量和过滤器中显示每个通道。 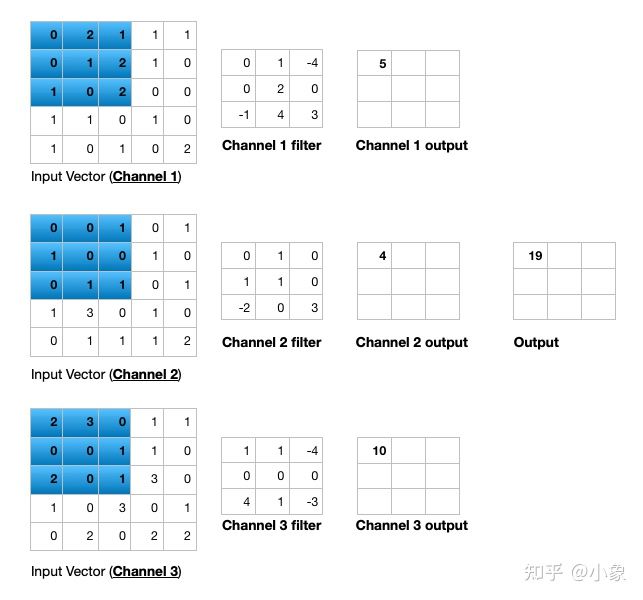图9 我们用一个更加直观的动图来看一下，下图显示了一个 3 维多通道 2D 卷积示例。 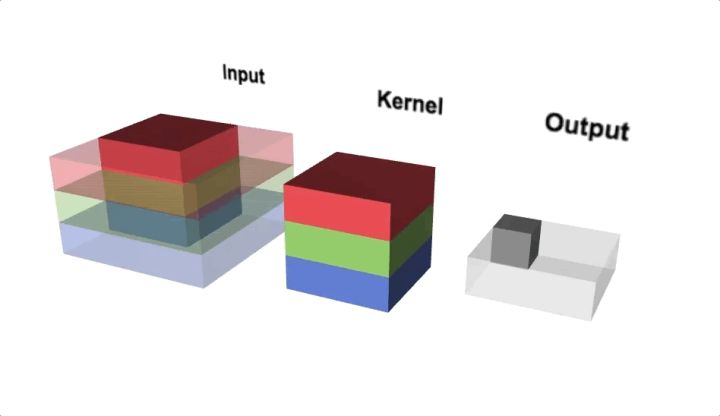图10 ### Pooling layer 池化层(pooling layer)执行下采样以减少输入的空间维度。这减少了参数的数量，从而减少了学习时间和计算量，以及过拟合的可能性。最流行的池化类型是最大池化(max pooling)。它通常是一个 2 x 2 的过滤器，步长为 2，当它滑过输入数据时返回最大值（类似于卷积过滤器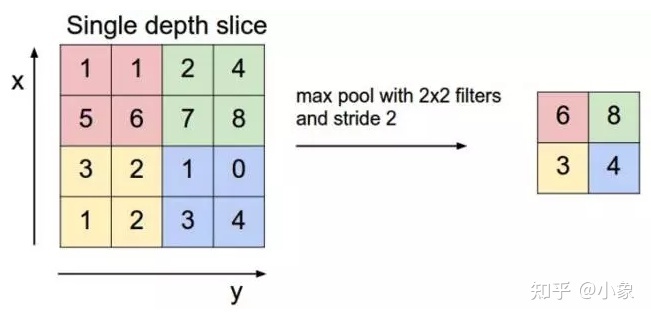）。 图11 ### Fully connected layer CNN 的最后一层是全连接层。我们将上一层的所有节点连接到这个全连接层，它负责图像的分类。 一个典型的 CNN 模型通常有不止一个卷积层或者池化层。每个卷积加池化层负责不同抽象级别的特征提取。例如，第一层中的过滤器可以检测水平、垂直和对角线边缘。下一层的过滤器可以检测形状，最后一层的过滤器可以检测形状的集合。过滤器值随机初始化并由学习算法学习。这使得 CNN 非常强大，因为它们不仅可以进行分类，还可以自动进行特征提取。这将 CNN 与其他分类技术（如支持向量机）区分开来，后者不能进行特征提取。 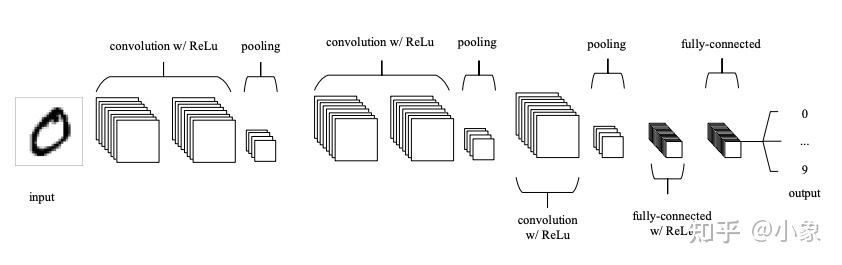图12 ## 练习 此示例使用 MNIST 手写数字。该数据集包含 60,000 个用于训练的示例和 10,000 个用于测试的示例。这些数字已经过大小标准化并以固定大小的图像（28x28 像素）为中心，值从 0 到 255。 在这个例子中，每个图像都将被转换为 float32 并归一化为 [0, 1]。 图13 首先导入用到的包 ```python import tensorflow as tf from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense, Dropout,Conv2D, MaxPool2D, Flatten
然后加载数据集
```python
mnist = tf.keras.datasets.mnist

(x_train, y_train), (x_test, y_test) = mnist.load_data()

可以打印数据集的shape看一下

print(x_train.shape)
print(y_train.shape)

输出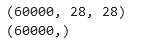： 图14 我们可以显示训练集中的一张图看看

import matplotlib.pyplot as plt
plt.imshow(x_train[0], cmap='gray')
plt.title('%i' % y_train[0])
plt.show()

如图所示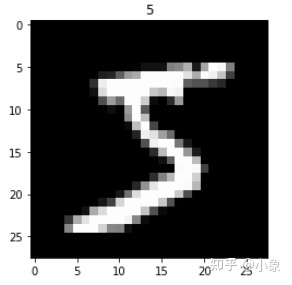： 图15 接着：

x_train = x_train.reshape((-1, 28, 28,1)).astype('float32')
x_test = x_test.reshape((-1, 28, 28,1)).astype('float32')
x_train = x_train / 255.0
x_test = x_test / 255.0

定义模型：

model = Sequential()
model.add(Conv2D(input_shape=(28, 28, 1), filters=32, kernel_size=(3,3), strides=(1,1), padding='valid', activation='relu'))
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Flatten())
model.add(Dense(10, activation='softmax'))

可以打印模型看看：

model.compile(optimizer=tf.keras.optimizers.Adam(),
             # loss = keras.losses.CategoricalCrossentropy(),
             # 损失函数多分类使用交叉熵(这里还要看标签是否为one-hot编码)
              #回归问题用均方差
             loss = tf.keras.losses.sparse_categorical_crossentropy,
             metrics=['accuracy'])
model.summary()

图16 模型训练：

history = model.fit(x_train, y_train, epochs=3, validation_data=(x_test, y_test))

展示训练过程中的loss：

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title("model loss")
plt.ylabel("loss")
plt.xlabel("epoch")
plt.legend(["train","test"],loc="upper left")
plt.show()

模型保存：

model.save('saved_mode/cnn1_save1.h5')

测试集评估：

model.evaluate(x_test, y_test) # 输入数据和标签,输出损失和精确度.

我们可以加载之前保存过的模型，对图像进行预测

#模型加载及自身数据预测
import tensorflow as tf
from tensorflow import keras
import tensorflow.keras.layers as layers
import cv2
import numpy as np
import matplotlib.pyplot as plt

#load model
model = tf.keras.models.load_model('saved_mode/cnn1_save1.h5')

def output(y_pre, y):
    temp = np.argmax(y_pre)
    print('预测结果为：' +str(temp))
    print('实际结果为：' +str(y))
    if str(temp) == str(y):
        print('预测结果正确')
    else:
        print('预测结果错误')

def readnum(path):
    img = cv2.imread(path, 0)
    img = cv2.resize(img, (28,28))
    plt.imshow(img, cmap='gray')
#     plt.title('%i' % y_train[0])
    plt.show()
    img = np.array(img)
    img = img.reshape((-1,28,28,1)).astype('float32')
    img = img / 255.0
    return img


test_file = 'testImage/5.png'
x_pre = readnum(test_file)
y_pre = model.predict(x_pre)
output(y_pre, 5)

输出效果如下： 图18